目的
Pythonによる株価のテクニカル分析ということで、ボリンジャーバンドについて紹介します。
Pythonのライブラリである「mplfinance」を使用することで、
簡単なコードで、ボリンジャーバンドのグラフを作成することが可能です。
そもそもボリンジャーバンドって何?というところから、具体的な分析方法まで紹介しています。
さらに、Pythonで実際にコードを書くことで、数式への理解が深まります。
ボリンジャーバンドとは?
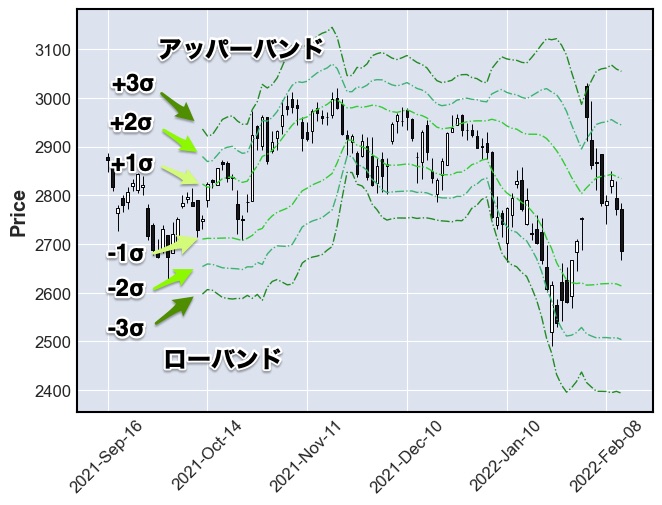
ボリンジャーバンドとは、移動平均の標準偏差σを加味したものであり、
チャートがバンドを突き抜けるのは非常に稀なケースだといえます。
統計学に基づいて計算された指標で、値動きがバンド内に収まる確率は以下の通りです。
移動平均の標準偏差
とても簡単にいうと、移動平均がどれくらいバラつく可能性があるかを示した値です。
価格がバンド内に収まる確率
- ±1σの範囲内に収まる確率 → 約68.3%
- ±2σの範囲内に収まる確率 → 約95.4%
- ±3σの範囲内に収まる確率 → 約99.7%
実行結果
ソースコード
下記のソースコードをコピーすることで、簡単にチャートを作成することができます。
準備&株価の取得
上記の実行結果を参考にしていただければ、問題ありませんが、
詳しいライブラリのインポートや株価の取得については、
下記の記事を参考にしていただければと思います。
ボリンジャーバンドによるテクニカル分析
ボリンジャーバンドのグラフを表示する関数
def BB(df, period):
#パラメータ設定
df['BBMA'] = df['Close'].rolling(window=period).mean()
df['BBSTD'] = df['Close'].rolling(window=period).std()
df['BBH1'] = df['BBMA'] + df['BBSTD'] * 1
df['BBL1'] = df['BBMA'] - df['BBSTD'] * 1
df['BBH2'] = df['BBMA'] + df['BBSTD'] * 2
df['BBL2'] = df['BBMA'] - df['BBSTD'] * 2
df['BBH3'] = df['BBMA'] + df['BBSTD'] * 3
df['BBL3'] = df['BBMA'] - df['BBSTD'] * 3
bbargs = dict(width=1, linestyle='dashdot')
#ボリンジャーバンドのグラフ設定
add_plot = [
mpf.make_addplot(df['BBH1'], **bbargs, color='limegreen'),
mpf.make_addplot(df['BBL1'], **bbargs, color='limegreen'),
mpf.make_addplot(df['BBH2'], **bbargs, color='mediumseagreen'),
mpf.make_addplot(df['BBL2'], **bbargs, color='mediumseagreen'),
mpf.make_addplot(df['BBH3'], **bbargs, color='forestgreen'),
mpf.make_addplot(df['BBL3'], **bbargs, color='forestgreen'),
]
#キャンドルチャートの作成
mpf.plot(df, type='candle', addplot=add_plot)パラメータ設定
df:取得した株価データフレーム
下記のパラメータは、商品、期間、使い方によって、自身で数値を考える必要があります。
period:株価データを参照する日数
グラフ説明
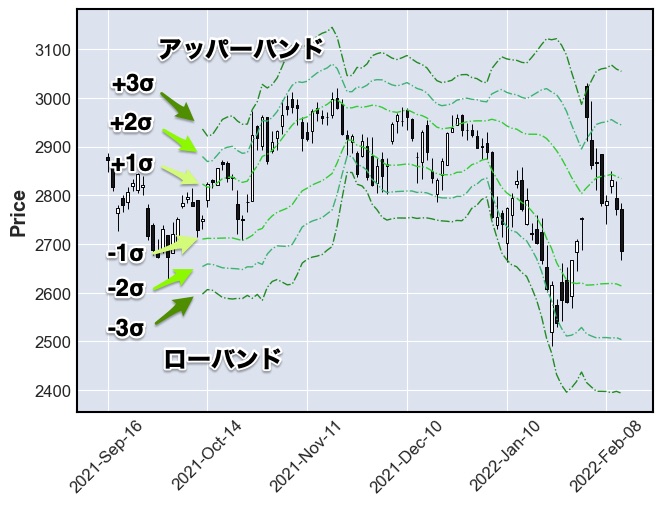
アッパーバンド :+1σ, +2σ, +3σ
設定した日数の移動平均 + 設定した日数の標準偏差 ×(1,2,3)
ローバンド:-1σ, -2σ, -3σ
設定した日数の移動平均 – 設定した日数の標準偏差 ×(1,2,3)
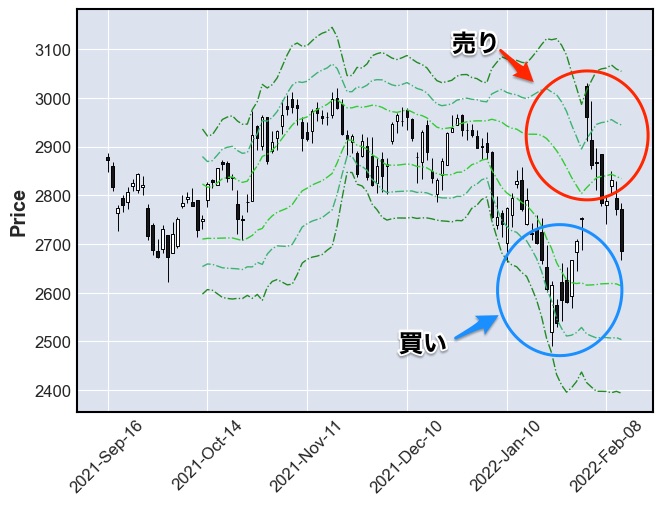
一般的な分析方法
- 上に抜けた時には高値になっているから売り
- 下に抜けた時には安値になっているから買い
価格がバンドを突き抜ける確率
- ±1σの範囲を突き抜ける確率 → 約31.7%
- ±2σの範囲を突き抜ける確率 → 約5.6%
- ±3σの範囲を突き抜ける確率 → 約0.3%
具体的なパラメータ
一般的なパラメータ(世界の投資機関がよく使用しているもの)
period:20日間
BB(df_stock_data,20)
ボリンジャーバンド_2σのグラフを表示する関数
def BB_2σ(df):
#パラメータ設定
df['BBMA'] = df['Close'].rolling(window=20).mean()
df['BBSTD'] = df['Close'].rolling(window=20).std()
df['BBH2'] = df['BBMA'] + df['BBSTD'] * 2
df['BBL2'] = df['BBMA'] - df['BBSTD'] * 2
bbargs = dict(width=1, linestyle='dashdot')
#ボリンジャーバンドのグラフ設定
add_plot = [
mpf.make_addplot(df['BBH2'], **bbargs, color='green'),
mpf.make_addplot(df['BBL2'], **bbargs, color='green'),
]
#キャンドルチャートの作成
mpf.plot(df, type='candle', addplot=add_plot, mav=20)グラフ説明
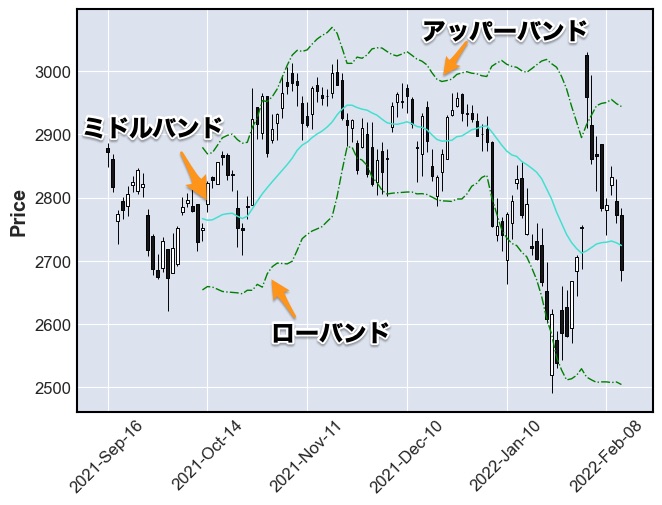
ミドルバンド:20日間移動平均
アッパーバンド:20日間移動平均 + 20日間標準偏差×2
ローバンド:20日間移動平均 ー 20日間標準偏差×2
分析方法
ボリンジャーバンド幅が狭い:標準偏差が低い→バラツキが小さい
ボリンジャーバンド幅が広い:標準偏差が高い→バラツキが大きい
参考にした本
テクニカル分析の方法だけでなく、
投資について、わかりやすく書かれているので、大変参考になると思います。
電子書籍の方が半額で購入できるので、そちらをオススメします。